Three Effective Techniques To Play Sudoku

Many people like to play Sudoku, but almost people don’t know how to play it. Follow these three effective techniques for Sudoku solutions.

1.  ELIMINATION ON SQUARES

The most obvious method involves finding a blank for which only one possible digit remains. For example, the highlighted square in grid A can’t hold a 6, 1, or 3, since those digits are already in its row. Nor can it hold the 4 or 7, since they are already represented in the highlighted square’s column. Likewise, the square can’t hold a 9, 5, or 2 because those numbers are already in its block. The only number from 1 to 9 that isn’t eliminated is 8, so the highlighted square must hold an 8.

More often than not, when you attempt this elimination method, you will be left with more than one possibility. If no more than three or four such possibilities exist, it can be very useful to lightly pencil in those possibilities in the blank.

2.  SOLVING ON POSSIBILITIES IN COMMON

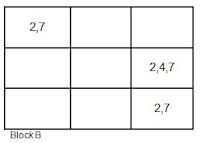
Suppose you have used the ‘elimination on squares’ method and have penciled in partial solutions for three of the blanks in a 3-by-3 block. Suppose further that the possibilities are: 2 and 7 for the first blank; 2, 4, and 7 for the second; and 2 and 7 for the third (see block B). Since the first and third each hold only either 2 or 7, they must hold 2 and 7, in some order. Thus, the second blank can’t hold either of those numbers – it would have to hold a 4.

Furthermore, none of the other six squares in the block can contain a 2, 4, or 7, so those numbers can be eliminated from their possibility lists. In general, if the combined possibility lists for three blanks in a row, column, or block include no more then three of the numbers from 1 to 9, then no other blanks in the row, column, or block can be any of those three numbers. Likewise for four lists with only four numbers, and so on.

3.  ELIMINATION ON NUMBERS

So far, our strategy has been to look for the only number that can be placed in a particular blank. Now we’ll use the complementary attack – look for the only blank that can hold a given number. An illustration will help express this idea. We know there must be a 5 in the third horizontal row of grid C. It won’t be in any of the three on the left, since a 5 already resides in the top-left block. Likewise, there can’t be a 5 middle three spaces of the third row. Finally, there can’t be 5 in the seventh spot of the third row, since we already have a 5 in the seventh column. By elimination, the 5 in the third row is in the eighth spot (just to the left of the 4).

Another way of doing elimination on numbers happens after you have used the ‘elimination on squares’ method and created lists of possibilities for all of the blanks in an entire row, column, or block. In this case, you may notice that only one of the lists includes the number 6. Thus, a 6 would have to go in that blank.

    Armed with these methods and others that you will undoubtedly come up with yourself, you will be solving Sudoku puzzles like a pro no time.